What is place value chart division?

The place value chart division method is a great way for introducing the division of larger numbers. My students have always responded well to this visual version of the box method and I find it helps those struggling to master division make more sense of how division works. I’ve found spending time on this method at the start of the topic means students grasp other more abstract methods faster and leads to improved accuracy overall.

Students will need a good foundation in partitioning numbers, I have some tips in this article that might help.

It involves breaking down multi digit numbers from the dividend into their place values. Each value is represented with manipulatives/visuals such as counters and base ten blocks.

Using the divisor, students can then determine how many groups there are in each value and what exchanging needs to be done to calculate the quotient. Having a visual representation of division with manipulatives creates a tangible learning experience, enabling students to explore and grasp this challenging concept.

How do you solve division problems with place value?

Let’s set up and work through an example with a 3 digit number divided by a 1 digit divisor:

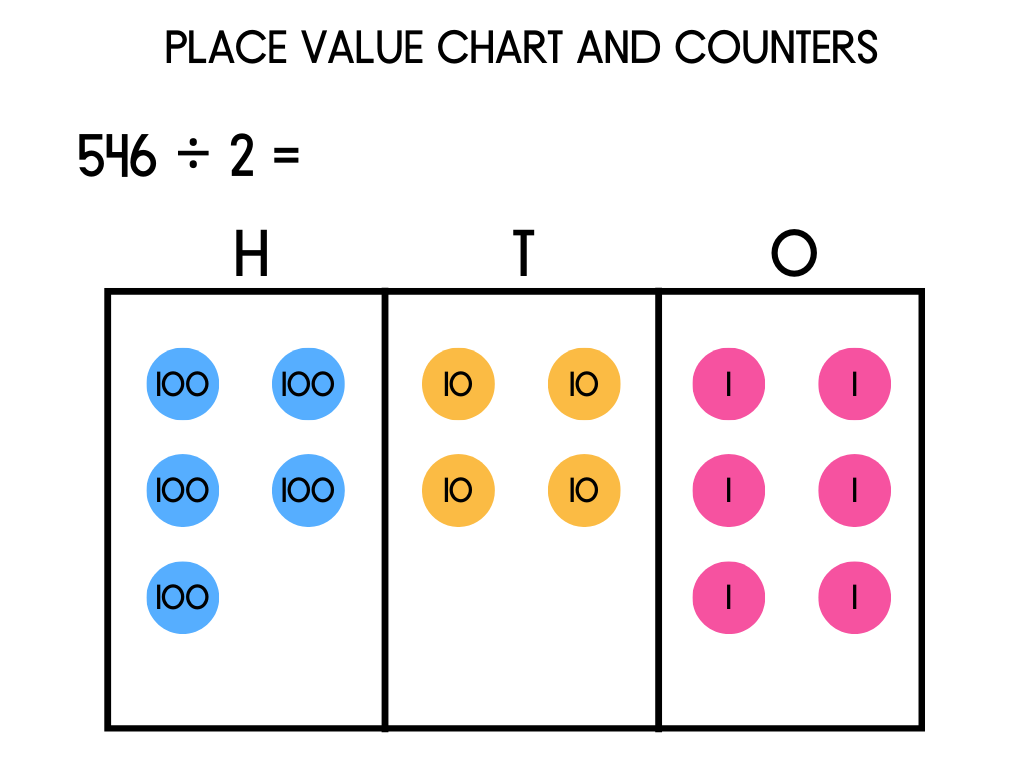
546 ÷ 2.

As our dividend (546) has 3 digits, our chart will need to have 3 columns to represent each place value.

In the example below, partition the 546.

546 = 500 + 40 + 6

Next use place value counters or base 10 blocks  (or draw dots if you don’t have manipulatives) to represent these values so 5 x 100 counters to represent 500 in the hundreds place, 4 x 10 counters to represent 40 in the tens place and 6 x 1 counters to represent 6 in the ones place.

Step 1

Start with the column on the left with the highest place value. In this example, the hundreds place.

Our divisor (2) tells us we need to group the counters into sets of 2.  Circle every set of 2 counters/dots that can be made. In this example, two whole sets of 2 counters can be made with one counter left over.

Write the number of sets made under the hundreds column.

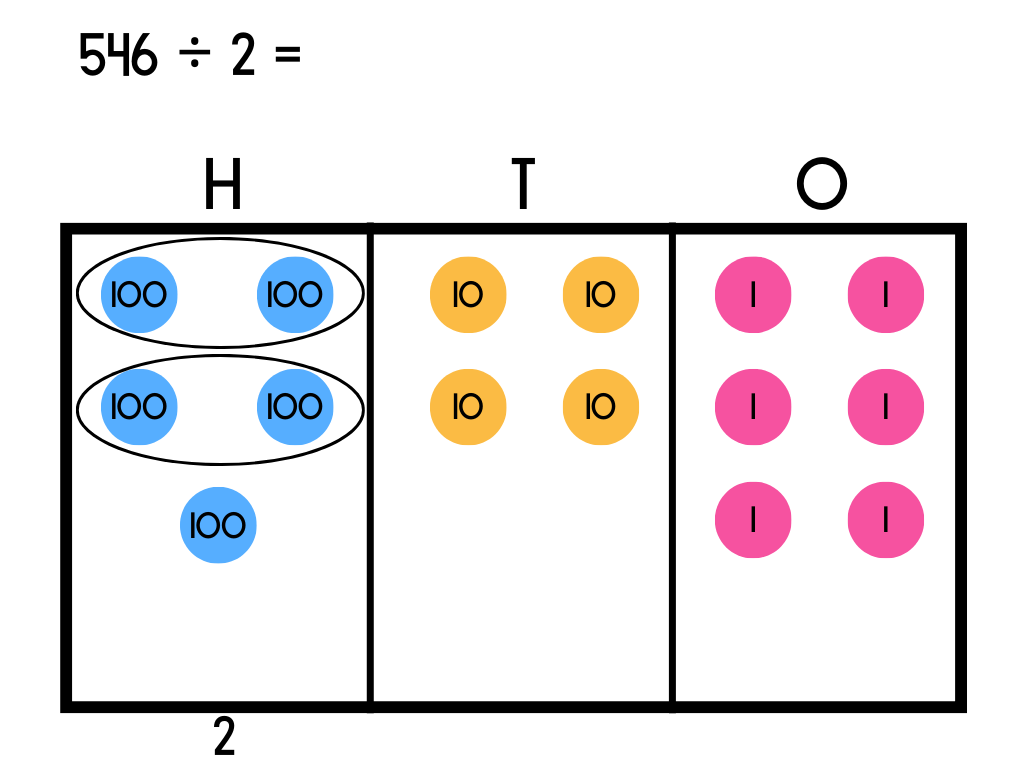
Step 2

The 100 counter that was left over will be moved up to the next place. A one hundred counter is worth ten of the 10s counters in the tens place. Exchange the 100 counter into tens. After exchanging the 100 counter into ten counters there is a total of 14 tens counters in the tens place.

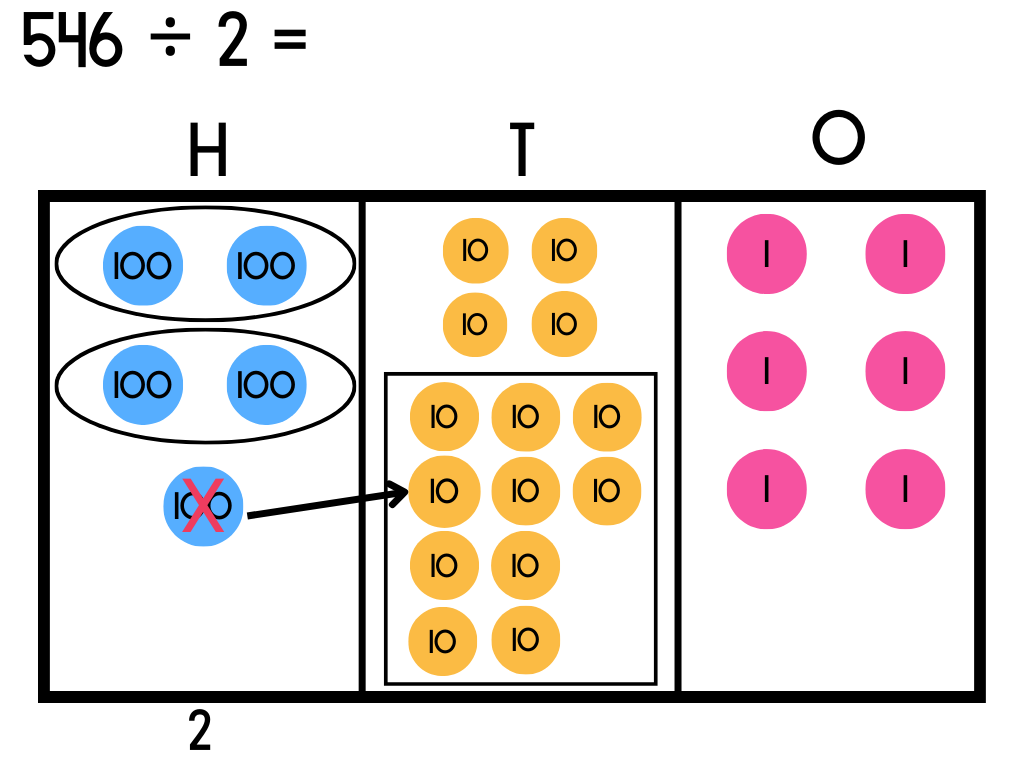
Step 3

We can now repeat the process of sorting the tens counters into sets of 2. There are seven complete sets altogether with no counters left over to move and exchange in the next place. Write the number of sets made under the tens column.

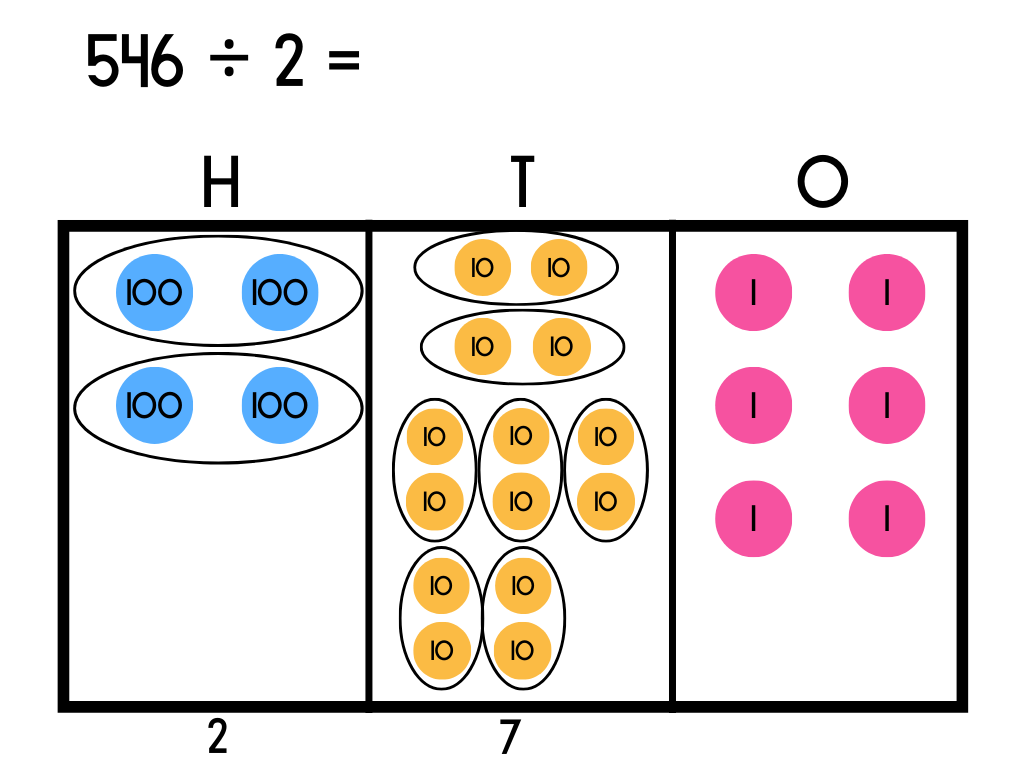
Step 4

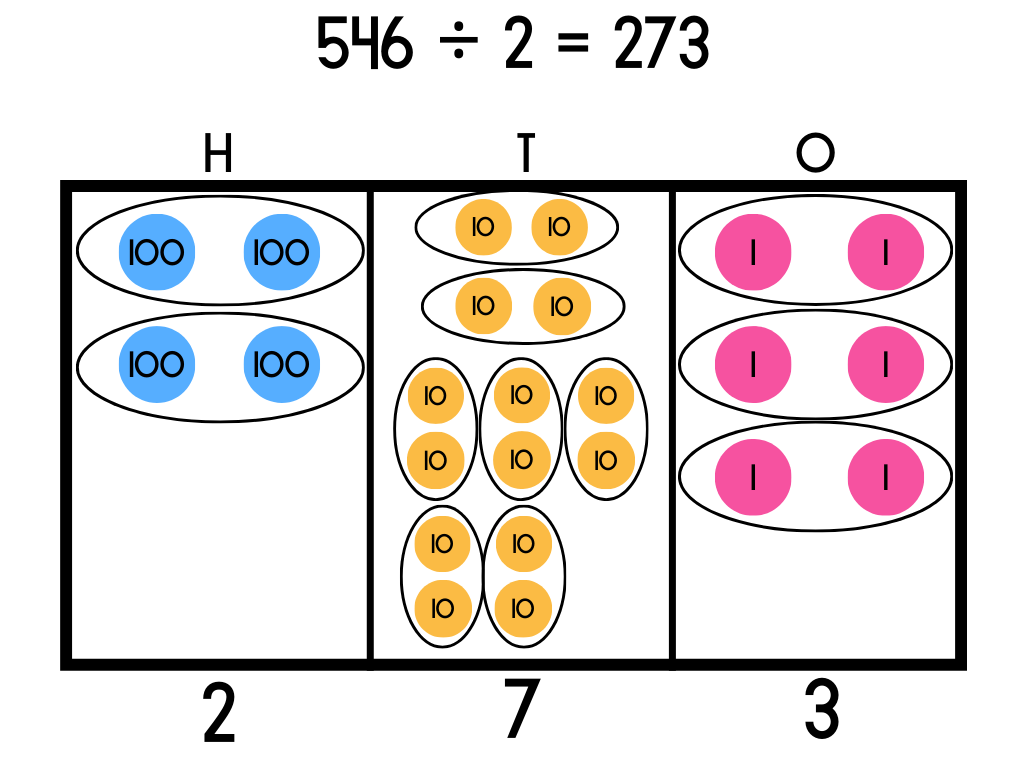
Repeat the process one more time again using the divisor 2 to determine how many counters go in each set. There are 6 ones counters, meaning 3 whole sets of 2 can be made. Write the 3 under the ones column.

If there were any ungrouped counters left over in the ones place, these would be written as a remainder.

Now all columns have been completed we can see the answer below the columns: 546 ÷ 2 = 273

A Few Quick Tips!

If using mini whiteboards for this activity, I find that it is helpful to not only model the calculation process but also how to record the answers on sheets or in notebooks. I’ve found students have worked through division equations effectively but no record of their work is available. For this reason, I have given this as a paired activity where one records an answer whilst the other student shows the calculation on the whiteboard. Remember to swap roles mid-way or on alternate problems.

As a next step in learning division, I would recommend using the box method for long division. The two together build really solid foundations in my experience.

As a starter or finisher, use an example where students have to spot an error. This is particularly useful if you are finding a common misconception or error.

Resources to support your teaching of long division

Jumping Elephant Math long division resources are designed to meet the needs of a variety of learners and align with common core standards. Check out these bestselling long division resources in my store.

I’d love to hear your thoughts and any tips you have for teaching this tricky area of math. Send me an email at – it would be great to hear from you!