The long division box method (or long division area model) is a systematic technique that I think is gaining more popularity when teaching long division. It’s certainly one of the methods I use.
It involves breaking down numbers from the dividend into their place values. The divisor sequentially divides into each place. Any remainders from the division are brought up to the next highest place value digit.
The benefit of this method is that it is highly organised and numbers are kept within their correct columns. It shares a comparable process with the standard approach. In standard long division, the process is Divide-Multiply-Subtract-Bring down-Repeat.
In contrast, the box method involves bringing up the remainder: Divide-Multiply-Subtract-Bring up-Repeat.
Step by Step Guide
In order for you to teach this method to your students, let’s work through an example with a 3 digit number divided by a 1 digit divisor. A FREE copy of this step by step guide is available from my store. Click here to download this useful resource.

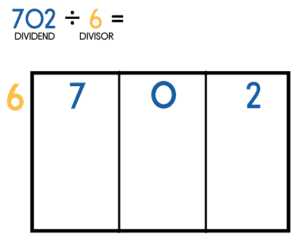
Set up the box for a long division question
In this first step, a rectangular box is drawn and divided into a number of sections. One section is needed for each digit of the dividend. In the example above we have a three digit dividend so 3 sections are needed in the box. Each digit of the dividend is written at the top of the sections. Our divisor (6) is placed on the outside of the box.
We are now going to go through each step of our process Divide-Multiply-Subtract-Bring up-Repeat.
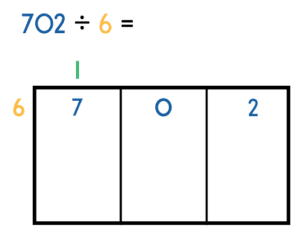
Step 1 – Divide
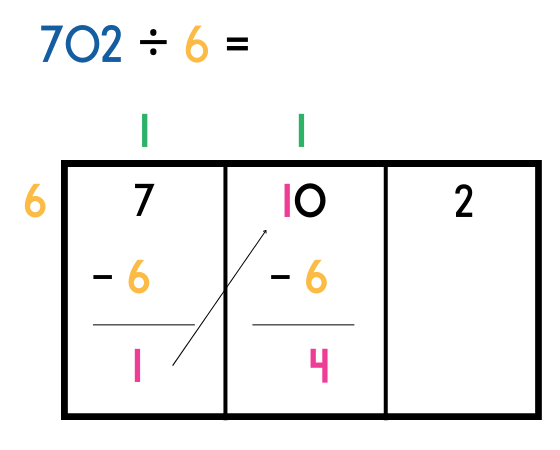
Start with the column on the left with the highest place value. In this example, the digit 7.
Ask the question how many whole groups of our divisor 6 go into this digit (7) without being more than 7. The answer is 1. Write this number above the section as shown in the diagram below.
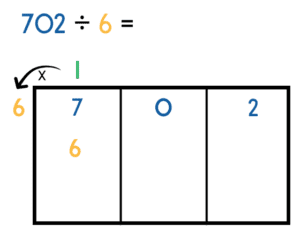
Step 2 – Multiply
Multiply the answer to the above step by the divisor. In our example it would be 1 x 6 = 6. Write this answer directly under the 7 as shown below.
Step 3 – Subtract
Subtract 6 from 7. Write the answer within the section as follows:
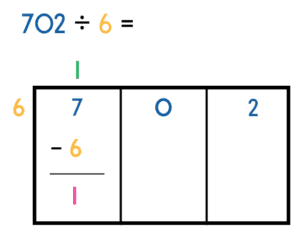
Our calculation shows 7-6 leaving 1 left over.
Step 4 – Bring up
Bring the answer to the subtraction up into the next section (slide along the arrow) and place this digit in front of the digit in this section. In our example 0 has now become 10.
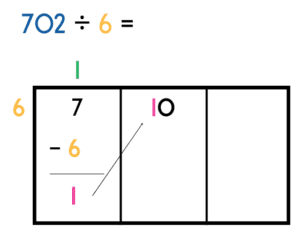
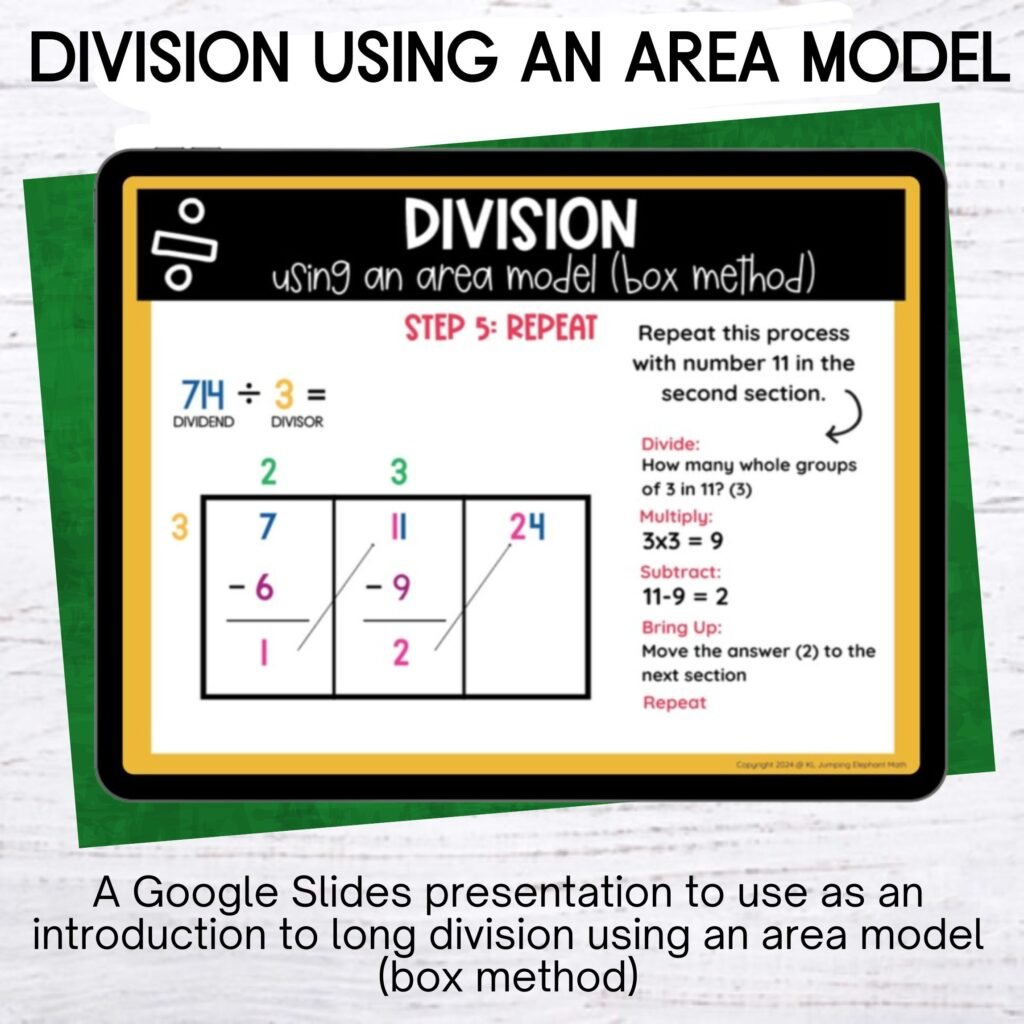
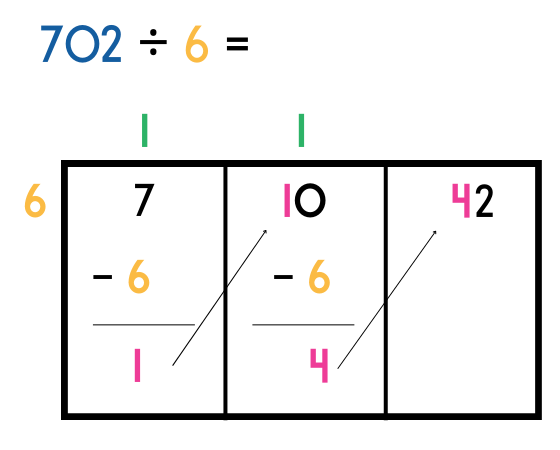
Step 5 – Repeat
You now need to repeat this process with the 10 in our second section and then continue until all sections have been completed.
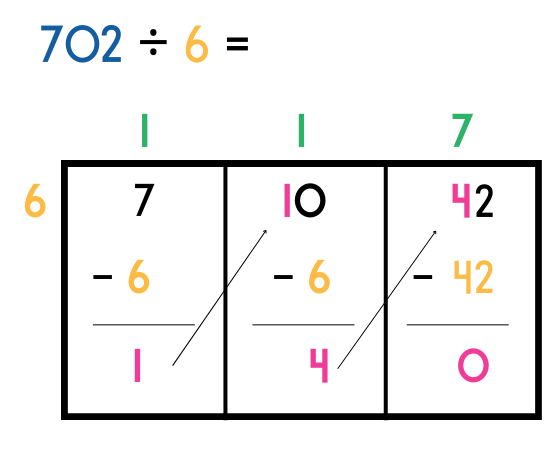
The answer to 702 divided by 6 = 117.
Box Method Resources
If you’re interested in practicing this technique, I’ve created box method division worksheets with editable templates to help students learn and reinforce understanding of this method.



This scaffolded resource includes 3 sets of box method division worksheets which are perfect for practicing 2 digit by 1 digit, 3 digit by 1 digit, and 4 digit by 1 digit division problems. Editable templates are included for each set along with answer keys.
Click here to visit my shop for further details
A few quick tips!
1. It can be helpful to have multiplication charts or divisibility rules in front of your students on their desks so that they can follow examples modelled. If you’d like a free copy of my divisibility rules poster and bookmarks, PLEASE CLICK HERE.
2. Scaffold the stages. Within my own class I start with 2 digit by 1 digit division problem to help students grasp the concept. As understanding grows, I gradually increase the difficulty.
3. Use templates where the boxes are set up and ready first (including arrows) before letting students. I’ve found it amazing how students can become preoccupied with drawing arrows and boxes and focusing on this as the learning point rather than the process of long division! It also helps students build accuracy
If you’d like to know more about other methods of teaching long division, please follow this link to read How to Teach Long Division to Upper Elementary.
Resources to support your teaching of long division
Jumping Elephant Math long division resources are designed to meet the needs of a variety of learners and align with common core standards. Check out these bestselling long division resources in my store.
I’d love to hear your thoughts and any tips you have for teaching this tricky area of math. Send me an email at katherine@jumpingelephantmath.com – it would be great to hear from you!