Long division is both challenging to learn and to teach! Students often have a broad range of understanding of this concept. It requires a strong prior understanding of all other operations: addition, subtraction and multiplication facts and methods, which may still be developing in many students.

Challenges

Upper elementary students need to understand that division is the inverse of multiplication. It requires more abstract thinking as it involves understanding and manipulating relationships between numbers in a way that goes beyond simple counting or concrete, tangible objects.

The steps involved in solving division problems are multiple and become more complicated with larger numbers. It can often be challenging for students to keep track of the steps.

Terminology can be difficult for students to master. The terms “dividend,” “divisor,” “product,” and “quotient” can overwhelm students, making it harder for them to discern the relationships between the operations.

So how do we as educators build solid foundations and make division accessible for upper elementary students?

The most straightforward answer is practice, practice, practice! I don’t believe there is a quick win when it comes to learning long division.

I try and fit in as much practice as possible in addition to timetabled lessons through activities such as exit tickets, a morning ‘challenge’ on the interactive whiteboard for students to do on arrival, looking for cross-curricular opportunities (can students write division word problems in an ELA lesson?) and using spiral math activities.

Mastering Math Facts

Knowing multiplication facts is crucial for division because division is the inverse operation of multiplication. Multiplication and division are reciprocal operations. If you multiply a number by a factor and then divide by that same factor, you return to the original number.

For example, if 8 × 5 = 40, then 40 ÷ 5 = 8.

I focus pre-learning activities on modelling this along with students and prepare math starter activities such as matching pairs where students match the inverse division and multiplication expressions.  

One way of helping to find factors to multiply is by using divisibility rules. Divisibility rules are shortcuts or guidelines that help determine if one number is divisible by another without performing the actual division.

Divisibility rules aid in identifying factors of a number. For example, if a number is divisible by 3, it means that 3 is one of its factors. This knowledge is valuable in various mathematical contexts.

To support your students I have a FREE resource available to educators. Please CLICK HERE to get a copy of the divisibility rules chart and divisibility rules bookmarks shown below.

Methods

There are different methods available when it comes to long division, each offering a unique approach to solving division questions. In this post, a selection of these methods, including the traditional approach, the box method, and the use of place value charts will be outlined.

Standard Algorithm – “Does MacDonalds Sell Cheese Burgers”

A helpful mnemonic for division steps is Does Macdonalds Sell Cheese Burgers where each letter represents one of the steps in the standard algorithm long division process.  

You can also add the word ‘Raw’ at the end of the mnemonic if you wish to represent ‘Repeat’. This is great for helping sequential recall and simplifying a complex process in an engaging way. I find it more helpful if you model an answer using these steps next to the diagram so that students have the process reinforced. It’s also a great way to demonstrate the inverse relationship between division and multiplication.

Alternatives to this are to teach a chant ‘divide, multiply, subtract, bring on down and bring it on back!’ or Dad (Divide), Mom (Multiply), Sister (Subtract), Brother (Bring down), Rover the dog (Repeat)

Alternative Methods

Short division

This is a compact version of long division which essentially doesn’t show the steps involved to calculate the answer. It makes for a more direct and quick calculation but is perhaps better suited for those confident in multiplication facts or for questions where the quotient is more apparent.

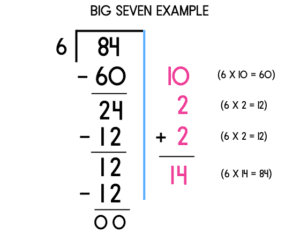
Big 7 Method

Some students may find the Big 7 method a useful way to calculate a division question, in fact many of my students prefer to start with this method along with the box method outlined below. It does simplify the process for students however a strong understanding of multiples is still needed. It relies more on students’ number sense and estimation skills.

The name comes from the fact that the division box looks like a big seven. Students take out groups of the divisor from the dividend. The partial quotients (The factor or the number with which the divisor is multiplied) are written to the right of the “Big 7” and added together to find the answer to the division question. Educators should encourage students to subtract what I call ‘friendly’ groups, such as double, or multiples of 5 or 10 at a time. For a detailed step by step guide to the big seven division method, please read this blog post.

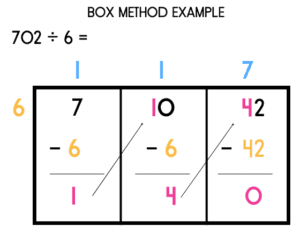
Box method

The box method of division, also known as the area model or grid method, is an alternative approach to long division. It involves creating a box or grid to visually represent the division process. If you would like to learn more about this method, please click here for a step by step guide.

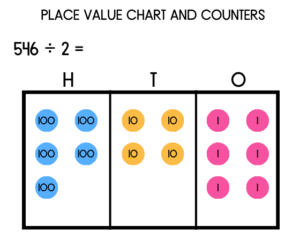
Place Value Charts and Counters

Another method for educators to try is using place value charts and counters. I find this is a great method for the diverse learning styles within a classroom. It supports visual and kinesthetic learners to understand how long division works. It also works well as a digital option (for example using Google Slides). It is however a time consuming method which becomes cumbersome when having to manipulate a large amount of counters. It isn’t widely used in standardized testing so it’s a method I use to support understanding before moving on to other methods. A step by step guide is available in this blog post.

In my opinion, it’s best to try a range of methods to cater for individual preferences. Wherever possible I teach the options available and allow students to find what works best for them and develop their division skills using their preferred method.

Resources

If you’re looking for some long division resources to support your teaching. Please visit my store by clicking on the images below.

Any comments or questions? Drop me an email at [email protected]